
How to Master GMAT Problem Solving
UPDATED FOR THE NEW GMAT IN 2024
To master GMAT Problem Solving, you’ll need to develop the following skills:
- A firm grasp of basic, high school math concepts
- The ability to avoid careless errors
- Good time management
- A flexible and creative mindset
Although GMAT Problem Solving questions are rooted in fundamental, high school-level math concepts, they often require a limber approach that you can’t find in any textbook. Our tips for GMAT Problem Solving will help you thrive on these questions – no matter what the exam throws at you.
What Topics Are Tested in GMAT Problem Solving?
The following are some of the most common math topics that appear in GMAT Problem Solving questions:
● Arithmetic ● Rates
● Algebra ● Probability
● Geometry ● Combinatorics
● Exponents ● Statistics
● Percents ● Number Properties
● Ratios
The first step to mastering GMAT Problem Solving is to develop accuracy on algebra, arithmetic, and number properties. Since those three topics appear in more than two-thirds of GMAT quant questions, students should give them priority when developing GMAT Problem Solving study plans.
Although many students obsess over the more exotic topics listed above (such as combinatorics, probability, and rates), these topics collectively represent less than 10% of GMAT Problem Solving questions. So if you need to make a big improvement in your GMAT Problem Solving performance, spend the bulk of your time developing your accuracy on algebra, arithmetic, and number properties.
Avoiding Careless Errors on GMAT Problem Solving
The GMAT is an adaptive exam, which means that when you answer GMAT questions correctly, the test will give you harder questions as you move through the section. If you get a bunch of easy Problem Solving questions wrong, on the other hand, your quant score will plummet. For this reason, avoiding careless errors on easy questions is essential to mastering GMAT Problem Solving.
The best way to avoid careless mistakes is to practice the following three steps on every GMAT Problem Solving question you tackle:
- Read carefully. Many students miss GMAT Problem Solving questions not because they fail to understand the math, but because they miss a key detail in the question.
- Plot an efficient path forward. There are usually several different ways to solve any given GMAT Problem Solving question. If you take a few moments to think through your options before jumping in, you’re more likely to choose an efficient path that avoids tortuous algebra and arithmetic – and you’re far less likely to make a careless error.
- Check your work as you go. Don’t wait until the end of the problem to check your work. By catching careless errors as soon as possible, you’ll make the best use of your precious time and energy. How to Master Time Management on GMAT Problem Solving
The best time management strategy for GMAT Problem Solving is to avoid wasting time on questions that you can’t solve efficiently. Because the GMAT is an adaptive test, most test-takers will answer 30-50% of all quant questions incorrectly – even if they ultimately get an excellent quant score. So you’ll need to be prepared to guess and move on when you’re overmatched by a GMAT Problem Solving question.
The best approach to GMAT Problem Solving is to read the question twice, and then plot your path forward towards a solution. If you think you’re on track for an efficient answer to the question, great – solve the question, double-check your work to avoid silly mistakes, and continue to the next question. But if you don’t see a good path forward on a GMAT quant question, then you’ll want to guess and move on quickly.
By following this strategy, you’ll spend the majority of your 62 minutes actually solving problems, and waste relatively little time clawing away at questions that you likely wouldn’t get right anyway.
Another benefit of good time management is that you won’t find yourself rushing towards the end of the section. Rushing often leads to careless errors, and as we’ve already discussed, careless errors will seriously damage your GMAT Problem Solving performance.
For more, check out this video on how to manage your time on adaptive tests like the GMAT.
Developing a Flexible Approach to GMAT Problem Solving
While a strong understanding of fundamental math concepts is essential, you’ll need more than just content knowledge to master GMAT Problem Solving. In fact, students often perform better on GMAT Problem Solving when they stop thinking of it as “math” and start thinking of it as “quantitative reasoning.”
For most high school students, math is taught as sequences of mechanical steps to be memorized and followed. GMAT Problem Solving questions, on the other hand, often come with a twist. By presenting familiar math topics in unfamiliar contexts, they challenge students to be both flexible and creative in their approach.
Consider the following problem as an example:
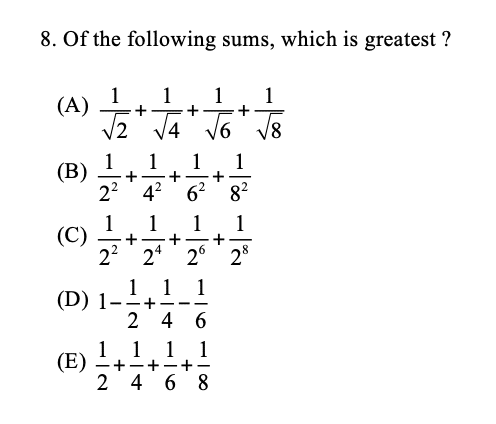
If you think of this as a mechanical “math question,” you’ll follow some well-worn steps here: find some common denominators, add the fractions, and THEN compare the sums. But if you’re thinking of the GMAT as “quantitative reasoning,” maybe you’ll try something quicker, smarter, and less arithmetic-intensive.
For instance, since we’re just looking for the greatest value, we don’t care what that value actually is. As long as we know that it’s larger than the other four expressions, we’ve found the correct answer. So since the question is asking for the greatest of the five answer choices, you can just compare pairs of answer choices, and knock off anything that’s the smaller of the two.
Let’s start with (D) and (E). It’s easy to see why (E) is larger than (D) once you notice that 1 – ½ = ½, so (D) is gone.
Similarly, (B) looks a lot like (E), except that the denominators in (B) are squared – and since larger denominators mean that the fractions must be smaller, we can cross off (B). The same argument holds for (C) – it’s clearly smaller than (E) as well. And then (A) has smaller denominators than (E) – so (A) is your answer.
Overall, if you’re thinking of GMAT Problem Solving as a set of narrow mathematical tasks, then you’re barking up the wrong tree. Once you start looking for opportunities to apply flexible logic and identify multiple solution paths, then you’re on the right track.
